あいかわらず等級が気になる
最近はPUIPUIモルカーとボートレーサーの等級審査のことばかり考えています。
前回、前々回も4月末までの競艇選手の等級審査について話題にしましたが、改めて等級についておさらいします。
ボートレース公式サイトから引用するとボートレーサーの勝率によって分けられている階級です。

他のサイトなどを見ると、勝率トップの選手からのヒエラルキーを示すため、ピラミッド図で等級を表しているのをよく見ます。
こんな感じですね。


あれ?でもこれなんか比率がおかしくない?

よく気付いたね。その通り。

A1が少なすぎるし、B2が多すぎるよね

そうだね。エリアの面積を人数比率と合わせるにはどうしたらいいかな。
久しぶりに三角関数
エクセルのSmartArtを使うとピラミッド図を簡単に描けるのですが、比率までは正しく調整できません。(目分量でなら等分以外に変更することはできます)
では
三角形全体=ボートレーサー全員(1600人)
A1=20%(320人)
A2=20%(320人)
B1=50%(800人)
B2=A1、A2、B1以外 =10%(160人)
ピラミッドの各エリアの面積とするとどうなるでしょう。
簡単な三角関数で計算してみました。
A1の三角形の高さを求める
作りたいピラミッドを1辺の長さが10の正三角形とします。下図のような形になるかと仮定しました。
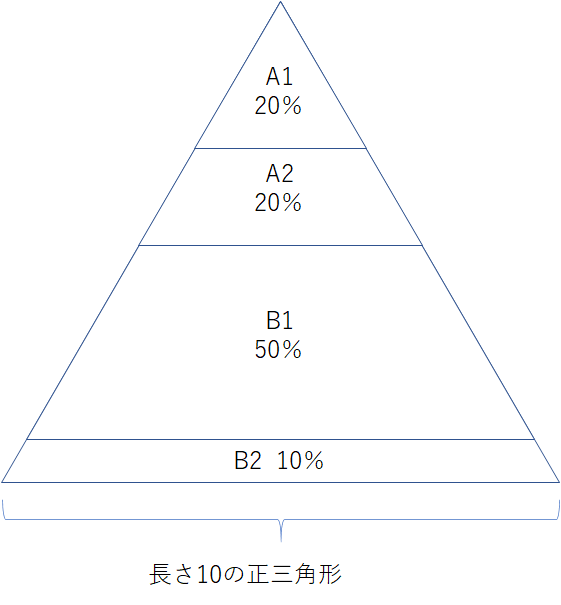
A1の三角形が全体の三角形の20%の面積になるためにはA1の底辺と高さを算出したいところ。そこで垂線をひきました。
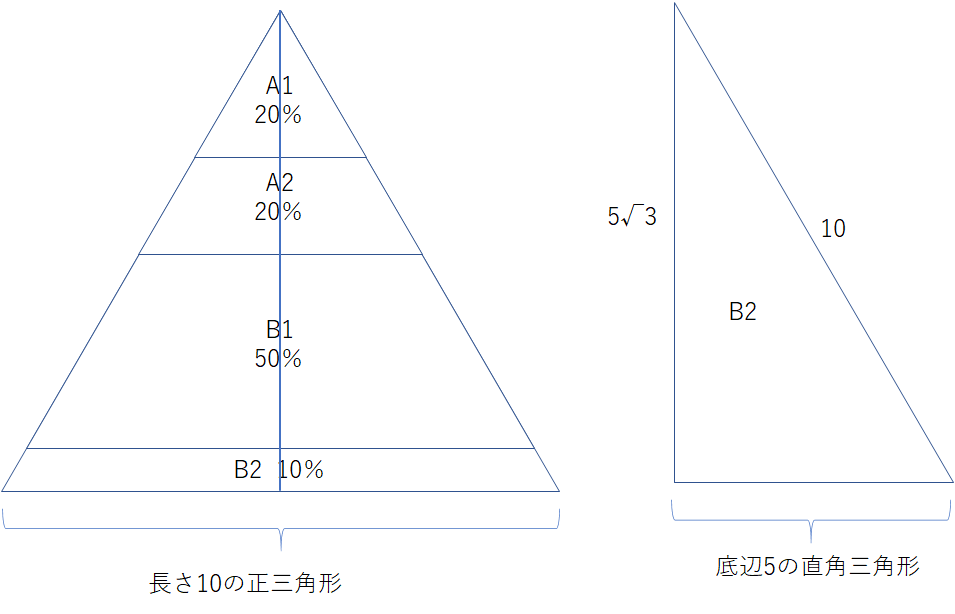
三平方の定理から全体の三角形の高さは$5\sqrt{ 3 }$ですね。
A1の三角形は全体の三角形の相似形です。
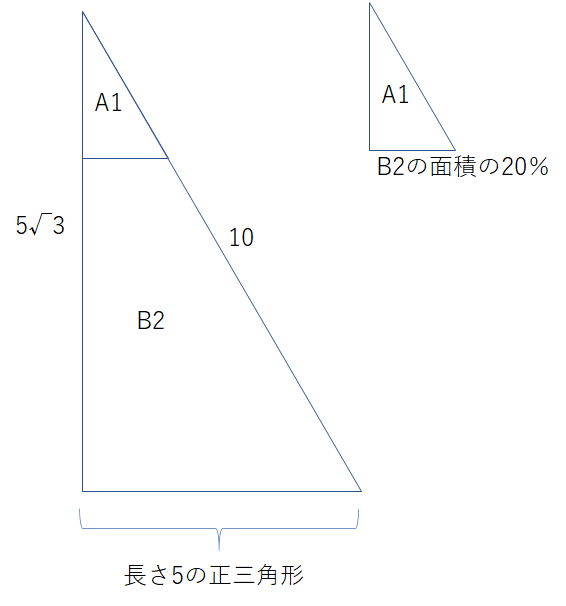
A1三角形の底辺を$x$とすると、高さは$\sqrt{ 3 }x$となるので面積の関係は以下となります。
$$5\sqrt{ 3 }*5*0.5*0.2=\sqrt{ 3 }x*x*0.5$$
展開すると
$$x^2=5$$
$$x=\sqrt{ 5 }$$
となります。でも今回知りたいの高さだった。
ということで高さは
$$高さ=\sqrt{ 3 }x$$
なので
$$高さ=\sqrt{ 15 }$$
となります。
つまり1辺の長さ10の正三角形の場合A1は頂点から引いた垂線の上から$\sqrt{ 15 }$のところまでの高さとなることがわかりました。
あとは同じ要領でA2、B1も高さを計算していきます。
正しい面積比率のピラミッド図を作った
各エリアの面積が人数と対比しているとすると正しいピラミッド図はこうなります。
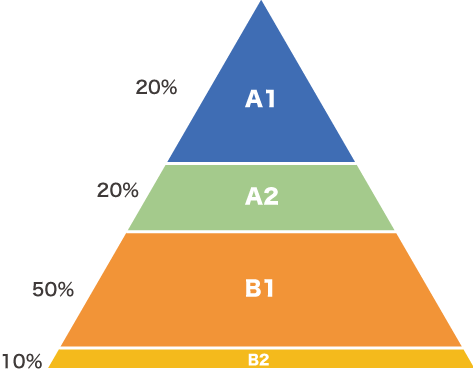
三角形って不思議で、A1とA2だとA1のほうが大きそうに見えますね。
今後ボートレーサーのランクをピラミッド図で説明する際は遠慮なくこちらをお使いください。
休日に何やってんだろうと思いました。
疲れた方にはモルカーを。



